Research
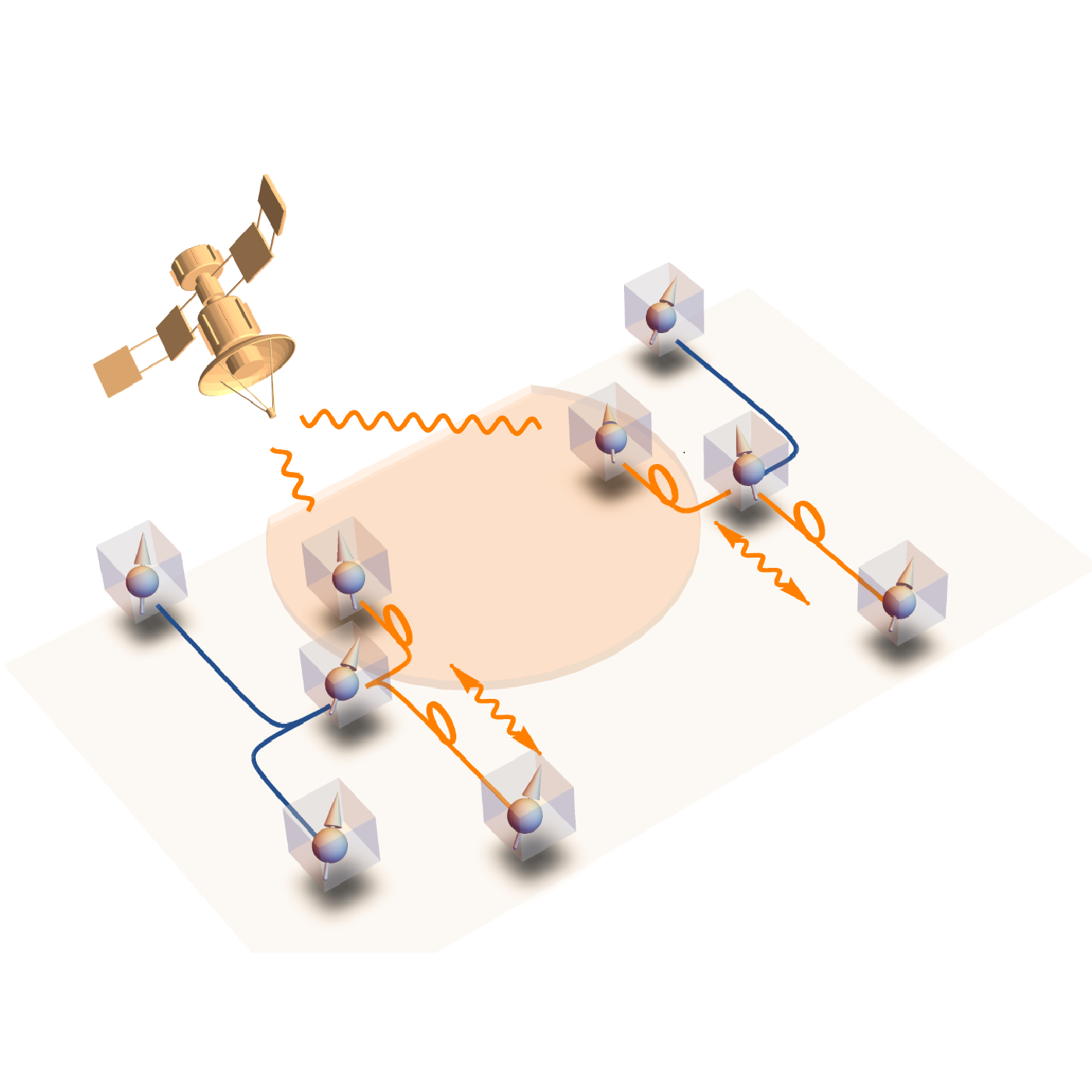
QUANTUM NETWORK
What will a future quantum network look like? How can we efficiently communicate and compute within such a network? Does the size of the network affect its connectivity and scalability? To answer these questions, it is essential to delve into the large-scale statistical behaviors of quantum networks—more deeply than ever before.
PHYSICAL NETWORK
What if a network has a shape? Using string theory, we explore the possibility of equipping a network with differential geometry, making the network a smooth manifold. We find that a minimization principle of not only the wiring length but also higher-dimensional manifold measures (such as surface area or volume) can explain some universal morphologies of biological systems that have long been observed, yet not theorized.
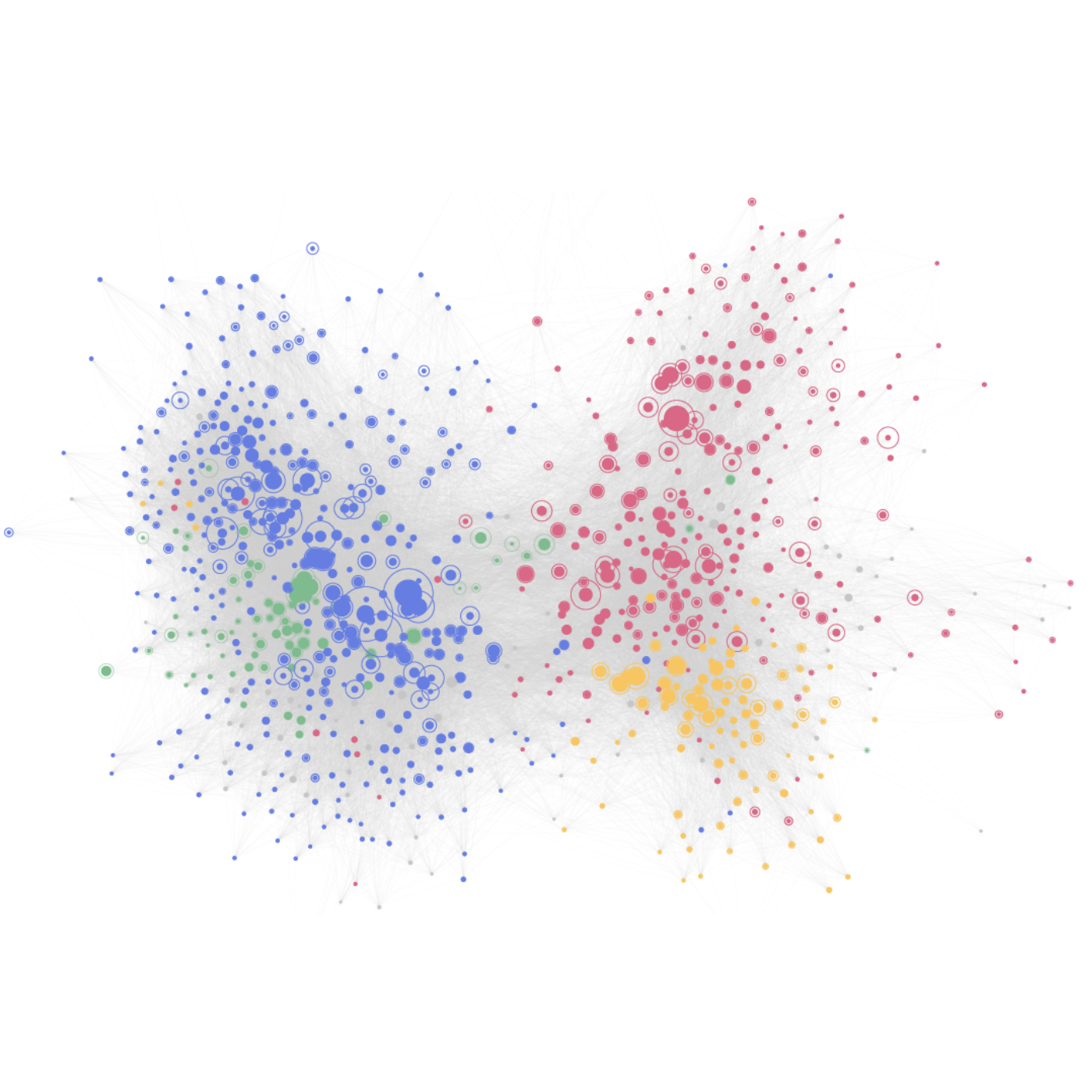
NETWORK OF PHYSICS
This network displays 880 foundational physics papers (Blue: high energy. Red: condensed matter. Yellow: quantum. Green: astrophysics. Gray: other fields) as nodes and halos. Node size corresponds to explicit citations, while halos represent hidden citations—representing clear textual credits to a discovery (e.g., general relativity) without references to the publication (Einstein’s 1915 paper) embodying it. Accounting for hidden citations allows us to uncover deeper connections between topics and reshape how we allocate scientific credit based on citation counts.
NETWORK OF NETWORKS
In many real-world systems, individual networks depend on other networks, forming interdependent networks. For example, a traffic network and a power grid may rely on each other: the power grid provides lighting for roads, while the traffic network enables maintenance of the power cables. We are interested in the structural and dynamical behaviors of such a network of networks, analyzing them using a rich set of tools, from percolation theories to dynamical equations.